Coordinate systems
Introduction
In the three dimensions of our world you can define different coordinate systems. In our auditory labs a subject is placed with his head in the center of the speaker setup (a sphere or semi-circle). We define the coordinate systems in this situation with respect to the default position of the head of the subject.
Normally we are interested in the direction of a stimulus and we define the directions with the angles azimuth and elevation in a double polar coordinate system. This system is a non-conventional coordinate system that is not often used beyond auditory experiments.
- Coordinates in 3 dimensions are normally described by triples e.g. [X, Y, Z] or [phi, theta, r].
- Coordinates systems are defined with respect to the default gaze position in the experiment.
- When stimulus positions are specified, the coordinates are expressed in double polar coordinates.
- Our EMF head tracking system uses three orthogonal axis: Horizontal, Frontal, Vertical. We refer to them as H, F and V.
- For a fixed Cartesian coordinate system in the lab we will adopt the coordinate system "HFV".
- Other fixed coordinate systems in the lab are Double Polar and Spherical coordinates.
- When we want to use a Cartesian coordinate system relative to the head we will adopt the medical coordinate system "RAS".
- Equipment with IMU's can have use different definitions for Cartesian coordinates and we will refer to X, Y and Z for data in coordinates defined by a device which has yet to be converted to HFV or RAS coordinates.
- Our Gitkab\biofysica toolbox has classes and transformation functions for HFV, RAS, Double Polar and Spherical coordinate systems.
- The use of coordinate systems and transformations between coordinates systems should be made explicit in all documentation and programs.
The Spherical Coordinate System is more standard and is widely used. When your are interested in the Spherical coordinate system you have to ask Wikipedia or other sources.
Cartesian coordinates in the lab
For the lab we use the "HFV" coordinate system:
- H stands for Horizontal and is positive to the right.
- F stands for Frontal and is positive in the forward direction.
- V stands for Vertical and is positive in the upward direction.
The orientation of H, F van V are defined by the default position (looking straight ahead) of the subject (tested person) sitting on the experimental chair in the lab. The [0, 0, 0] position is right between the test persons ears.
In terms of unit vectors: V = H x F
Medical Cartesian coordinates
For a body (or head) a medical notation is often adopted:
left (L) right (R) anterior (A) posterior (P) superior (S) inferior (I)
For describing the position of the head of a person we will adopt the 'RAS'-convention:
R-axis: from left (-R) to right (+R) A-axis: from back (-A) to front (+A) S-axis: from bottom (-S) to top (+S)
The origin in this system is chosen again right between the ears.
In terms of unit vectors: S = R x A
Double Polar coordinates
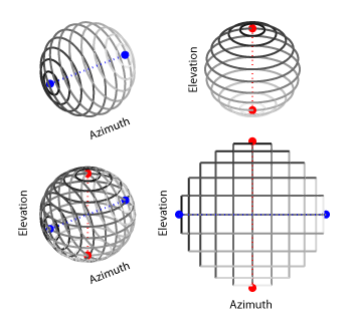
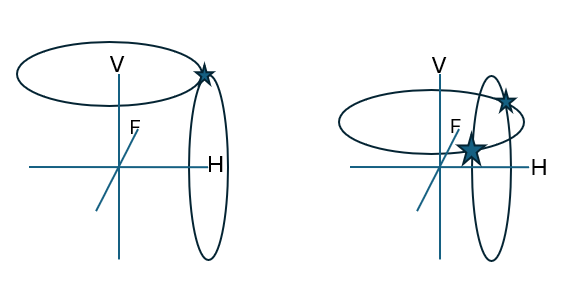
The double polar coordinates are fixed in the lab. The coordinates are called azimuth , elevation and radius. The azimuth defines a semi-circle parallel to the FV-plane. The elevation defines a circle parallel to the RF-plane. The intersection of the azimuth circle and the elevation circle is the target point. Since there are two intersections (most of the time), the hemisphere of the intersection has to be specified in order to resolve the ambiguity (see left picture). Often only elevation and azimuth is given, assuming the target is in the forward hemisphere and the radius is not relevant.
- pictures: Azimuth and elevation determine two perpendicular circles.
azimuth
- Azimuth is the angle with the FV-plane.
- pi/2 <= azimuth <= pi/2 (or -90° <= azimuth <= 90°)
elevation
- Elevation is the angle with the RF-plane
- pi/2 <= elevation<= pi/2 (or -90° <= elevation <= 90°)
radius
- Radius is the distance from the origin to a target point.
- In our lab experiment the radius is not important and can be set to 1.
hemisphere
- Pictures: The stars mark the intersections of the circles. When the circles touch (only one intersection) the target lies in the HV-plane.
- Hemisphere is +1 for a point in the forward hemisphere.
- Hemisphere is 0 for a point in the HV-plane (F=0).
- Hemisphere is -1 for a point in the backward hemisphere.
consistency check
There is a constraint on azimuth and elevation:
azimuth + elevation <= pi (or azimuth_deg + elevation_deg <= 90°)
Transforming double polar to HVF coordinates
H = radius * sin(azimuth) V = radius * sin(elevation) F = hemisphere * sqrt(radius^2 - H^2 - V^2)
Transforming Cartesian to double polar coordinates
In the origin we have by definition azimuth = 0 and elevation = 0.
radius = norm([H, V, F]) azimuth = arcsin(H/radius) elevation = arcsin(V/radius) hemisphere = sign(F);
Matlab
Angles
Standard trigonometry functions in Matlab use radians as unit for angles. Inside your programs it is advised to use only radians in the code and convert to degrees when presenting values for angles on screen, or in an output file. When reading from screen or input file you should convert degrees to radians at the first assignment.
- When variables use degrees they should have the suffix _deg in the name.
- It is recommended to use the matlab conversion functions between radians and degrees:
angle = deg2rad(angle_deg) angle_deg = rad2deg(angle)
Trigonometric functions
Matlab has all kind of standard trigonometric functions working with radians or with degrees. When degrees are used it is recommendable to add the suffix "_deg" to your angle variables.
Standard trigonometric functions using radians:
x = sin(angle) x = cos(angle) x = tan(angle) angle = asin(x) angle = acos(x) angle = atan(x) angle = atan2(y, x)
Standard trigoniometric functions using degrees:
x = sind(angle_deg) x = cosd(angle_deg) x = tand(angle_deg) angle_deg = asind(x) angle_deg = acosd(x) angle_deg = atand(x) angle_deg = atan2d(y, x)
Coordinate system representations
In the Gitlab in biofysica\utilities\coordinates\RAS_DP_SPH there are classes for the coordinates
coordinates_HVF.m coordinates_HVF_withID.m coordinates_RAS.m coordinates_DP.m coordinates_DP_withID.m coordinates_SPH.m coordinates_SPH_withID.m
The classes with suffix "_withID" are meant for relating coordinates to IDs of Leds or Speakers.
HVF coordinates are the coordinates fixed in the lab. It has the following fields:
- ID (optional) - right or H (in meters) - up or V (in meters) - forward or F (in meters)
In our auditory experiments the default position is the reference orientation and the origin is taken between the ears of the subject.
RAS coordinates is the standard for coordinates relative to the head orientation. It has the following fields:
- right or R(in meters) - anterior or A (in meters) - superior or S(in meters)
Double Polar coordinates
- ID (optional) - azimuth (in radians) - elevation (in radians) - radius (in meters) - hemisphere (+1, 0 or -1: stands for forward, in between or backward hemisphere)
Spherical coordinates
- ID (optional) - azimuth (in radians: 0 to 2pi positive X-axis is 0) - elevation (in radians: -pi to pi positive Y-axis is 0) - radius (in meters)
Example code:
right = 0.5; % in meters anterior = 0.5; % in meters superior = 0.5; % in meters % create a stimulus position in RAS: stimulusPos_RAS = coordinates_RAS(right, anterior, superior); % transform the stimulus position from RAS to double polar: stimulusPos_DP = transform_RAS2DP(stimulusPos_RAS);
Coordinate transformations
Lab coordinates: DP <==> HVF
The biofysica repository has the following transformation functions:
and conversion functions between coordinates:
transform_HVF2DP transform_DP2HVF transform_device2RAS
They all have a single input parameter in the form of a struct or table and a single output parameter in the form of a table. Angles are always in radians.
- HVF2DP_withNetCalibrationFile (Field coil reading to Double Polar)
The HVF2DP has an extra parameter NetCalibrationFile, that should contains the filename of the latest calibration.
Device ==> RAS
In order to transform device XYZ-coordinates to RAS-coordinates you have to specify a 3x3 transformation matrix.
E.g. If the X-saxis is pointing to Superior, the Y-axis to Right and the Z-axis pointing to Anterior you get the following transformation matrix:
XYZ2RASdefinition = [0, 1, 0;
0, 0 ,1;
1, 0, 0];
With the defined transformation matrix you can use the transform function:
RAScoordinates = transform_XYZ2RAS(XYZcoordinates, XYZ2RASdefinition)
An example is definition_EyeSeeCamSci_XYZ2RAS.m which defines the transformation matrix for the EyeSeeCamSci.
Built in Matlab functions for rotating Cartesian triples
For rotations of Cartesian coordinates Matlab uses a 3x3 matrix working on the XYZ column vector. For rotations around an axis there are functions that create these 3x3 matrices. It is important to know if the rotation axis is defined with respect to the room or with respect to a rotating device like a head tracker.
In the biofysica toolbox you have the functions Rx, Ry and Rz. These functions generate rotation matrices. Mx = Rx(angle1) My = Ry(angle2) Mz = Rz(angle3) In case the rotations are small (say smaller than 1 degree) the order is not important: M = Mx * My * Mz When the rotation is done in multiple small steps you have: M(i) = Mx(i) * My(i) * Mz(i) And for the total rotation you have two situations depending on the coordinate system in which Mx, My and Mz are defined. rotations in the device coordinates: M_total(i) = M(i) * M_total(i-1) rotations in the room coordinates: M_total(i) = M_total(i-1) * M(i) -------------------------------------------------------------------------------------- if you have the Aerospace Toolbox you can use rotx, roty and rotz (angles in degrees) Mx = rotx(angle1_deg) My = roty(angle2_deg) Mz = rotz(angle3_deg) -------------------------------------------------------------------------------------- You can perform a rotation by applying the rotation matrix to a column vector (point = [1;0;0]) newPoint = M * point;
Older biofysica functions
N.B. These are not recommended for new code.
Here are some earlier functions that are using different conventions:
varargout = azel2cart(AZ,EL,R) azel = cart2azel(x,y,z) azel = xyz2azel(x,y,z) [PostRotAZ,PostRotEL] = rotate2d(azimuth,elevation,Beta) [X,Y,Z] = pitch(X,Y,Z,Angle) [X,Y,Z] = yaw(X,Y,Z,Angle) N.B. all angles are in degrees
Stimulus position lookup tables
Setups with different speaker and led positions have a lookup table for the stimulus positions in the form of an excel file. The excel file should have a sheet with the name 'DP' for data in double polar coordinates. The sheet should have five columns with the headers 'ID', 'azimuth', 'elevation', 'radius', 'hemisphere'.
stimulusPos = readtable(fname, 'sheet', 'DP');
The function 'readtable' outputs a table with the named column headers that are accessable in the same way as fields of a struct.
ID = stimulusPos.ID; azimuth = stimulusPos.azimuth; etc....
Head tracking
Field coil head tracking
Field coil head tracking is a method for movement detection. A pickup coil mounted on the head of the subject is picking up modulated magnetic fields. Three lock-in amplifiers splits the signal from the head coil into three components, horizontal, vertical and frontal. These components are measured as voltages.
The convention for head tracking directions (H,V,F) are related to gaze in the following way:
Horizontal: H = positive signal when looking right Vertical: V = positive signal when looking up Frontal: F = positive signal when looking forward
In Gitlab (biofysica\utilities\coordinates\HVF_RAS_DP_SPH\HVF field calibration) there is a function 'convert_HVFfieldValues2DP_withNetCalibration.m' that uses a netcalibration file in order to transform the (H,V,F)-voltages into double polar coordinates.
Head tracker with IMU
Each head tracker with an IMU has its own XYZ coordinate system. In order to transform this to RAS coordinates we have to use a device specific transformation matrix. In the biofysica toolbox there is a function for each device (definition_XYZ2RAS_<devicename>) that generates a struct with a description of the definition for the XYZ2RAS transformation and a transformation matrix. This struct can be readily used as the input for the function transform_XYZ2RAS.
Here is an example of a transformation of XYZ coordinates to RAS coordinates of a head tracking device:
%get X, Y and Z from the device (X, Y and Z can be column arrays) X = get_X_fromTheDevice; Y = get_Y_fromTheDevice; Z = get_Z_fromTheDevice; % create a XYZcoordinates object XYZcoordinates = coordinates_XYZ(X,Y,Z); % transform to RAS coordinates RAScoordinates = transform_XYZ2RAS(XYZcoordinates, definition_XYZ2RAS_devicename); % this is what you get R = RAScoordinates.right A = RAScoordinates.anterior S = RAScoordinates.superior
Conventions for expressing angles in text
An angle is normally expressed in radians or degrees.
One radian corresponds to the angle for which the arc (s) on a circle equals the radius (r), thus 1 rad = s/r = 1. In the SI standard 1 rad = 1 per definition, so rad is dimensionless. Therefore it is not necessary to explicitly use it. Only when confusion is possible you should mention it as the unit behind a value.
The other convention for angles is the degree. The conversion between radians and degrees follows from the relation 360° = 2π rad. Note that the degree, with the symbol °, is not a unit of the SI. When expressing angles in degrees the use of the symbol ° is mandatory.
When using trigonometric formulae you have to be aware that by default these functions use radians. If you want to use constants expressed in degrees you have to use the degree symbol °. The following expression are equivalent:
X and L in meters, angle in radians X = L * sin(pi/2) is equivalent to: X = L * sin(90°) and angle = pi + arcsin(Y/L) is equivalent to: angle = 180° + arcsin(Y/L)